How this Article Began
Dear Reader,
I probably would not be writing this if the link had not been taken down. When I first opened it in my inbox, it was a Youtube video of someone explaining a scientific article published in NCBI in March, 2021. This was not your typical junky anti-Covid message. NCBI is the National Coalition Building Institute of Rochester, N.Y., Inc. This is a not-for-profit corporation, affiliated with NCBI International, whose mission is to eliminate racism and all forms of oppression and discrimination. The article was archived in PubMed Central, a source I have often used for my own medical research. The title of the article, which can be found here, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7996517/ was Outcome Reporting Bias in Covid-19 mRNA Vaccine Clinical Trials. For someone like me, this was golden.
Immediately interested, I began following along but something interrupted me. When I returned to it a day or two later, I was dismayed to find that the video of a PubMed article had been taken down. This article was not your run of the mill conspiracy theory video, but a legitimate scientific paper that was being explained to a lay person. Fortunately, I had recorded the title of the publication and was able to search for it online. I then proceeded to do my own analysis of the Covid vaccine research data to unearth what could have been so controversial about this article as to cause it to be taken down from Youtube.
The article itself is a very dry read on Absolute Risk Reduction (ARR) vs. Relative Risk Reduction (RRR) of the mRNA Covid-19 vaccines, but the conclusions are anything but dry. The concepts, however, are difficult to grasp, even for doctors since most of them have no research training. One needs to have knowledge and experience in clinical research and willingness to spend the time to conduct and explain a statistical analysis. Since I have invested the time, I am about to explain ARR and RRR because any consent to any intervention must be properly informed. In other words, informed consent means that one must be told and must understand everything about a treatment or procedure before consenting to it. This is the law in most countries where it would also apply to Covid-19 vaccination.
Absolute Risk Reduction (ARR) and Relative Risk Reduction (RRR)
Why are ARR and RRR very important? Very simply, let’s assume you have 100 people in a Treatment group and another 100 people in a Control or placebo group. Then, let’s say that 2 people get Disease X in the Control group while one person gets Disease X in the Treatment group. The Relative Risk Reduction or RRR in this example is 50% because one diseased person is 50% or half of 2 diseased people. However, the Absolute Risk Reduction (ARR) is only 1% because in the treatment group, only one fewer people out of 100 participants got Disease X. You can also work it out using these formulas:
- In the Treatment group, 1/100 got Disease X = 1% which is the EER (Experimental Event Rate)
- In the Control or placebo group, 2/100 got Disease X = 2% which is the CER (Control Event Rate)
- ARR (Absolute Risk Reduction) = CER – EER = 2% – 1% = 1%
In a subtraction the % signs carry through the equation and are kept.
- RRR (Relative Risk Reduction) = ARR divided by CER = 1% divided by 2% = ½
In a division, the % signs cancel each other out and are not kept, but ½ is the same as 50%.
Let’s say the Treatment in this example had side effects, as most treatments do. If a patient were offered this Treatment and was told that the “efficacy” (how well the treatment works) was only 1% (the ARR) which is the true efficacy, this patient would be much less likely to accept the Treatment and its side effects than if he or she were told the efficacy was 50%. Fifty percent sounds a lot more promising than 1% but it reflects only the comparison between the diseased people of each group. The ARR or 1% efficacy is much more accurate as it reflects how many more people out of 100 will be protected from Disease X as a result of the Treatment. To just say that the Treatment is 50% effective in this scenario by ignoring the ARR is to introduce outcome reporting bias.
Applying ARR and RRR to Pfizer’s mRNA Covid-19 Vaccine Data
Now let’s apply these formulas to Pfizer’s data as presented in their product monograph, the whole of which can be found here https://www.pfizer.ca/sites/default/files/202105/Pfizer-BioNTech_COVID-19_Vaccine_PM_EN_252524_19-May-2021.pdf) Section 14 discusses the methodology and analysis of their data, but note that this is a product monograph, a synopsis, and not the full scientific paper, which is more difficult to find. I have copied section 14 below, highlighting key areas in yellow and added my own comments in red.
Section 14.1 Trial Design and Study Demographics
The safety and efficacy of Pfizer-BioNTech COVID-19 Vaccine were evaluated in a Phase 2/3 randomized, placebo-controlled, multicentre study in participants 12 years of age and older. Based on data accrued through November 14, 2020, a total of 43,651 (21,823 in the Pfizer- BioNTech COVID-19 Vaccine group and 21,828 in the placebo group) (this is the initial number of participants at the onset of the study) Participants were randomized equally to receive 2 doses of Pfizer-BioNTech COVID-19 Vaccine or placebo separated by 21 days (19-23 days, per protocol). Randomization was stratified by age: 12 through 15 years of age, 16 through 55 years of age, or 56 years of age and older, with a minimum of 40% of participants in the ≥ 56-year stratum.
The study excluded participants who were immunocompromised and those who had previous clinical or microbiological diagnosis of COVID-19 disease. (Despite this, many health authorities are currently vaccinating many immunocompromised patients as well those who had previous Covid-19 disease) Participants with pre-existing stable disease, defined as disease not requiring significant change in therapy or hospitalization for worsening disease during the 6 weeks before enrolment, were included as were participants with known stable infection with human immunodeficiency virus (HIV), hepatitis C virus (HCV) or hepatitis B virus (HBV).
The primary endpoint was defined as any symptomatic COVID-19 case confirmed by Reverse Transcription-Polymerase Chain Reaction (RT-PCR). (The study did not measure how many lives this vaccine saved. It measured how many cases of Covid-19 infection this vaccine prevented) The population for the analysis of the primary efficacy endpoint included participants who did not have evidence of prior infection with SARS-CoV-2 through 7 days after the second dose (first primary efficacy endpoint), as well as participants with and without evidence of prior infections with SARS-CoV-2 through 7 days after the second dose (second primary efficacy endpoint). Participants are planned to be followed for up to 24 months, (The vaccine was approved for use prior to the end of the 24 month trial with no long term data available. Trial data is still being collected along with real world data) for assessments of safety and efficacy against COVID-19 disease.
Table 8 presents the specific demographic characteristics in the studied population.
Table 8: Demographic Characteristics – Subjects Without Evidence of Infection Prior to 7 Days After Dose 2 – Evaluable Efficacy (7 Days) Population (Data Accrued Through November 14, 2020)
| Pfizer-BioNTech COVID-19 Vaccine (Na=18,242) n (%) |
Placebo (Na=18,379) n (%) | Total (Na=36,621) n (%) | |
| Sex Male Female |
9318 (51.1) 8924 (48.9) |
9225 (50.2) 9154 (49.8) |
18,543 (50.6) 18,078 (49.4) |
| Age at Vaccination (years) Mean (SD) Median Min, max |
50.6 (15.70) 52.0 (12, 89) |
50.4 (15.81) 52.0 (12, 91) |
50.5 (15.76) 52.0 (12, 91) |
| Age group 12-15 years 16-55 years >55 years ³65 years |
46 (0.3) 10,428 (57.2) 7768 (42.6) 3980 (21.8) |
42 (0.2) 10,507 (57.2) 7830 (42.6) 4038 (22.0) |
88 (0.2) 20,935 (57.2) 15,598 (42.6) 8018 (21.9) |
| Race White Black or African American American Indian or Alaska native Asian Native Hawaiian or other Pacific Islander Multiracial Not reported |
15,110 (82.8) 1617 (8.9) 118 (0.6) 815 (4.5) 48 (0.3) 448 (2.5) 86 (0.5) |
15,301 (83.3) 1617 (8.8) 106 (0.6) 810 (4.4) 29 (0.2) 402 (2.2) 114 (0.6) |
30,411 (83.0) 3234 (8.8) 224 (0.6) 1625 (4.4) 77 (0.2) 850 (2.3) 200 (0.5) |
| Ethnicity Hispanic or Latino Not Hispanic or Latino Not reported |
4886 (26.8) 13,253 (72.7) 103 (0.6) |
4857 (26.4) 13,412 (73.0) 110 (0.6) |
9743 (26.6) 26,665 (72.8) 213 (0.6) |
| Country Argentina Brazil Germany South Africa USA |
2561 (14.0) 1232 (6.8) 121 (0.7) 287 (1.6) 14,041 (77.0) |
2539 (13.8) 1223 (6.7) 126 (0.7) 279 (1.5) 14,212 (77.3) |
5100 (13.9) 2455 (6.7) 247 (0.7) 566 (1.5) 28,253 (77.1) |
| Pfizer-BioNTech COVID-19 Vaccine (Na=18,242) n (%) |
Placebo (Na=18,379) n (%) | Total (Na=36,621) n (%) | |
| Comorbidities1 Yes No |
8432 (46.2) 9810 (53.8) |
8450 (46.0) 9929 (54.0) |
16,882 (46.1) 19,739 (53.9) |
a 1
N = Number of subjects in the specified group, or the total sample. This value is the denominator for the percentage calculations.
Number of subjects who have 1 or more comorbidities that increase the risk of severe COVID-19 disease: e.g. asthma, BMI ≥30 kg/m2, chronic pulmonary disease, diabetes mellitus, hypertension.
14.2 Study Results
Efficacy in Participants 16 Years of Age and Older (Based on Cut-off Date of November 14, 2020)
The analysis of the first primary efficacy endpoint (population without evidence of infection prior to 7 days after dose 2) included 36,523 participants 16 years of age and older (18,198 in the Pfizer-BioNTech COVID-19 Vaccine group and 18,325 in the placebo group). (These are the numbers in the control and vaccine groups towards the end of the study. Reduced numbers towards the end of a study is a typical occurrence. The numbers are still sufficient for analysis.) At the time of the final primary efficacy analysis, participants had been followed for symptomatic COVID-19 disease for a median of 2 months, corresponding to 2,214 person-years for the Pfizer- BioNTech COVID-19 Vaccine and 2,222 person-years in the placebo group.
There were 8 confirmed COVID-19 cases identified in the Pfizer-BioNTech COVID-19 Vaccine and 162 in placebo groups, respectively, for the first primary efficacy analysis. In this analysis, compared to placebo, efficacy of Pfizer-BioNTech COVID-19 Vaccine in participants with first COVID-19 occurrence from 7 days after Dose 2 (participants without evidence of prior infection with SARS-CoV-2) was 95.0% (95% credible interval of 90.3% to 97.6%). In participants 65 years of age and older without evidence of prior infections with SARS-CoV-2, efficacy of Pfizer-BioNTech COVID-19 Vaccine was 94.7% (two-sided 95% confidence interval of 66.7% to 99.9%). In the second primary efficacy analysis (participants 16 years of age and older with or without evidence of prior infection with SARS-CoV-2), compared to placebo, efficacy of Pfizer-BioNTech COVID-19 Vaccine in participants with first COVID-19 occurrence from 7 days after Dose 2 was 94.6% (95% credible interval of 89.9% to 97.3%). (Pfizer uses the term “efficacy was 95%” but makes no distinction between RRR (relative risk reduction) and ARR (Absolute Risk Reduction). In addition, there is no statistical analysis provided to explain how the investigators arrived at a 95% “efficacy” rate. This is the source of Pfizer’s outcome reporting bias.
*Case definition: (at least 1 of) fever, new or increased cough, new or increased shortness of breath, chills, new or increased muscle pain, new loss of taste or smell, sore throat, diarrhoea or vomiting.
Related Posts:
Analysis of Pfizer’s Data
- In the vaccine group, 8/18,198 got Covid-19 infection (not death) = 0.044%
This is the EER (Experimental Event Rate)
- In the Control (placebo) group, 162/18,325 got covid-19 infection (not death ) = 0.884%
This is the CER (Control Event Rate)
- ARR (Absolute Risk Reduction) = CER – EER = 0.884% – 0.044% = 0.84% = 0.84/100 = 0.0084
- RRR (Relative Risk Reduction) = ARR divided by CER or 0.84% divided by 0.884% = 0.95
As this formula involves division, the percentage signs cancel out. 0.95 is the same as 95% which is what the Pfizer study reports for “efficacy.” An “efficacy” of 95% gives the impression that one is 95% less likely to catch Covid-19 if one is vaccinated with Pfizer’s Covid-19 vaccine. However,
- the ARR or Absolute Risk Reduction, which is 0.0084 or 0.84%, is actually less than 1%
As shown under the ARR and RRR heading above, the ARR (of any study) is far more accurate than the RRR, but clearly, 95% sounds much more compelling than <1%. Referring to the “efficacy” of the Pfizer vaccine as 95% is not technically incorrect, but it is very misleading as this value does not properly inform the vaccine recipient. Such misrepresentation is at the very least unethical and at most illegal in many countries which require informed consent. Unfortunately, it is easy for outcome reporting bias to escape detection since the average individual, including the average doctor, does not understand ARR and RRR and will automatically assume that “95% efficacy” means 95% less likely to get Covid-19 in the real world.
Another way of understanding the ARR is by calculating the number needed to treat, or the NNT. The NNT in this case would be the number of people who would need to be vaccinated to prevent ONE case of Covid-19 infection (not death, since the study did not measure death) Here is the calculation:
- NNT = 1/ARR = 1 divided by 0.84% = 1/0.0084 = 119 people.
Note how 1/119 is also less than 1%
If we extrapolate an NNT of 119 to a population of 330 million, assuming the entire population of the USA were vaccinated with the Pfizer Covid-19 vaccine, 2.77 million Covid-19 infections (not deaths) would be prevented.
Analysis of Covid-19 Death Prevention
To date, there have been 33,217,718 Covid-19 recorded cases in the US and 593,282 recorded Covid-19 deaths. These statistics can be found here https://covidusa.net/ and their validity assumes that Covid cases have not been underestimated and Covid deaths have not been overestimated. If 2.77 million Covid-19 cases had been prevented by fully vaccinating every US citizen, the US would still have experienced approximately 30,447,780 Covid infections and by extrapolation 543,810 Covid deaths, a reduction of 49,472 deaths or 1.78% fewer Covid-19 deaths.
“CDC data also show that Americans, regardless of age group, are far more likely to die of something other than COVID-19. Even among those in the most heavily impacted age group (85+), only 13.3 percent of all deaths since February 2020 were due to COVID-19.”
A similar analysis of Moderna’s raw data which can be found in their product monograph here https://covid-vaccine.canada.ca/info/pdf/covid-19-vaccine-moderna-pm-en.pdf, shows a Relative Risk Reduction of 94%, an Absolute Risk Reduction of 1.2%, and a NNT of 83. In other words, Moderna’s Covid-19 case prevention is only marginally better than Pfizer’s.
From experience, we already know that self-isolation (staying home) when symptomatically ill, appropriate distancing and appropriate masking are more effective than less than 1%, the protection afforded by a Covid-19 vaccine. Otherwise, countries would not have been able to control this pandemic to any extent prior to the introduction of any vaccine.
Compared to providing Covid-19 protection, these mRNA vaccines are much more effective in enriching their already wealthy pharmaceutical producers, or those who have heavily invested in them. For the public good, it would have made more sense, saved more money, more time and possibly more lives to have put research efforts into other potential Covid-19 treatments, such as Ivermectin, Melatonin, Vitamin D, even the highly controversial Hydroxychloroquin, or anything else that has shown any indication of being helpful either as a prevention or a cure. Unfortunately, these are all inexpensive drugs with no hope of any appreciable returns for the pharmaceutical industry which relies on new innovations to garner profits, even if those innovations are of minimum benefit with the potential to cause great harm.
Here, I am not referring to harm from side effects, but harm from misplaced trust in a product that provides more side effects than it does protection. Justification for any treatment is found only when the benefits outweigh the risks. A quick look at the side effect rates in the tables of Pfizer’s and Moderna’s product monographs shows that although not life threatening in the studies, mild, moderate and severe side effects occurred with greater frequency than the <1% protection afforded by the Covid-19 Pfizer vaccine or the 1.2% protection afforded by the Moderna vaccine.
Implications Going Forward
Having executed this exercise, it no longer puzzles me that governments and public health departments continue to recommend social distancing, mask wearing, business closures and all the usual restrictions even for those who have had both doses of a Covid-19 vaccine. The public has also been told that there is no evidence that vaccination guarantees the prevention of Covid-19 spread or prevention. We now understand why this is true. At least the public is not being lied to all the time.
Historically, pandemics eventually run out of steam, killing off the vulnerable, not affecting those who are resistant and rendering natural immunity to the rest. Could some drug companies possibly be trying to profit as much as possible while this pandemic is still with us, and when it’s all over, take the credit for ending it? After all, we are being told that the only long-term solution to this pandemic is – immunization – but… is that true even with a <1% or 1.2% effective vaccine? Absolutely not.
Does this mean we will be required to re-immunize everyone indefinitely to prevent this pandemic from resurfacing? With vaccines that have such low efficacy, that is precisely what we may be required to do. In fact, it has already begun. Having barely finished giving our citizens their second dose, new recommendations are already emerging for booster doses of Covid-19 vaccines for the upcoming fall season. The public is already being forewarned that booster shots may be needed for a long time yet to come. Indeed, reaching herd immunity with any vaccine that has such a low efficacy would take a very, very long time. The natural infectivity of Covid-19 will achieve herd immunity much sooner and when the end of this pandemic finally comes – the vaccine will take a bow.
The low efficacy of the Covid-19 vaccines also explains why Covid-19 antibody test results include a caveat that antibody testing is meaningful only after having a Covid-19 infection and not a Covid-19 immunization. It makes sense that a <1% or 1.2% protection rate would result in a negligible antibody production rate, so why bother wasting public health dollars conducting a pointless antibody test?
And what does all this mean about the much talked about vaccine passports? Well, imagine a plane filled with (recall that Pfizer’s NNT = 119) 119 X 2 = 238 passengers, all of whom never had Covid-19 infection but all of whom got a Covid-19 vaccine. According to Pfizer’s data, only two of those travelers would actually be protected from Covid-19 if they got Pfizer’s vaccine. According to Moderna’s data, one in 83 or 2.5 people would be protected if they got Moderna’s vaccine. This low vaccine efficacy not only renders vaccine passports completely pointless but is a strong indicator that relying on them for public safety poses a great threat. A much better and safer approach for travelers would be a negative Covid-19 test, whose accuracy, although not perfect, is far better than 1% or less.
Conclusions:
Vaccination with a poor vaccine is not the panacea that will end the pandemic and bring us all back to normal. I could go on forever about the socioeconomic, ethical and legal implications of a highly ineffective vaccine that is being touted as a world savior by playing on public ignorance, fear and fatigue. The bottom line is: If people are properly informed that their ineffective protection from a Covid vaccine is actually 1% or less, and not 95% as advertised, vaccine uptake would drop dramatically, and in this particular instance, it should. Then, we can free ourselves, our energies, time and resources, to pursue better public health recommendations that utilize good scientific research to focuses on other more meaningful breakthroughs, including but not limited to any other much better vaccine in the fight against this, and any future pandemic.
As a medical researcher, a purist who searches for factual truths, I find this type of large-scale public exploitation and manipulation by the pharmaceutical industry for personal gain, utterly deplorable. What is even more alarming is how the vast majority of my well-intentioned but misguided medical colleagues have fallen hook, line and sinker for the vaccine rhetoric and are now falling over each other to immunize one another and thousands of equally poorly informed individuals with a vaccine that has an ARR of 1% or less. Words cannot express my dismay for our centers of medical research, licensing bodies and other medical bodies, have abandoned evidence-based medicine in favor of “trust” in a misguided rhetoric, even threatening disciplinary action against any physician who refuses a Covid-19 vaccine.
As I watch my once very reliable, logical and evidence-based scientific world disintegrate, sinking into ignorance and mass madness, my only hope is that the divine intervention of our Creator will restore us back to some semblance of normal, because vaccines such as these certainly will not.
Robert Williams, MD, PhD – Medical Researcher and Member of the Orthodox Church in America
The use of Absolute Risk Reduction vs. Relative Risk Reduction is completely botched by the author. He calculates the Absolute Risk Reduction during a vaccine trial (conducted at a time between surges when Covid infection was relatively low), then extrapolates that across all other time periods despite those time periods being far longer than the study and Covid infection rates being far higher. That’s not how Absolute Risk Reduction works at all – it is only applicable to the exact circumstances of the study and can’t be extrapolated to a different length of time with a different infection rate. That’s what Relative Risk Reduction is for.
…….
For comparison, let’s pretend we vaccinated half of a 100,000 strong army against anthrax. That gives us 50,000 vaccinated, 50,000 not vaccinated. Over the next year, 1000 of those soldiers equally divided between vaccinated/unvaccinated were sent into a battlefield where they were hit with a biological attack. 80% of the unvaccinated soldiers died (400) and 8% of the vaccinated soldiers died (40). The relative risk reduction across the entire army would be 90%, as 90% fewer vaccinated soldiers died than unvaccinated. But the Absolute Risk Reduction across the entire army would be just 0.72%, because the actual risk of death for a vaccinated soldier is less than 1%, mostly because 99% of them were never exposed to anthrax in the first place.
……
Let’s say the next year the entire army is sent into the battlefield, and ALL of them are exposed to anthrax in another biological attack. Can you use that 0.72% Absolute Reduction Risk to determine how many lives vaccination will save? Of course not! That Absolute Risk Reduction was contingent on only 1% of the soldiers being exposed in that previous time period, it is completely meaningless in the new situation where everyone is exposed. That’s exactly what Relative Risk Reduction is for.
……
I see that several others have already pointed this out to the author. And he ignored all of them. I’m flabbergasted. If he truly has a PhD in a medical field, has he shown this to any of his colleagues or professors? They would be able to correct him immediately.
How did you come up with this idea? All data was from the product monograph and so would be for the clinical trial period. That was clearly stated.
As others note, 20X less infection rate vaccinated to not.
With an Rt>1 that is not a good thing.
And: plunging infection rates bely the fact that the vaccine is actually effective.
Hospitals are clearing out their ICU’s.
The vaccines are demonstrably effective.
20x less infection, but at what cost / benefit? That was also a primary point of the article. You are reducing infection rates against the placebo, but in the real world that comes at the cost of side effects and the opportunity cost of having invested billions in costly vaccines when cheaper alternatives could have saved money and lives. We have every reason to believe the cheaper drugs are actually more effective. If you told the truth to people, “We are going to inject you with experimental drugs for which we have no long-term track record, and which we did not test on major groups of people, to slightly reduce your chances of getting a disease for which you have a 99.9% chance of surviving…” – how much uptake do you think you would get? Not much, which is why they never phrase it that way.
As for real world effectiveness, Covid is a seasonal and endemic disease. That is why the rates were dropping earlier in the year before vaccines could make any appreciable difference. We published this back in April:
You could further look at the vaccine uptake rates among U.S. States. There are states with low uptake, yet they are not doing any worse than those with high vaccination rates. https://www.beckershospitalreview.com/public-health/states-ranked-by-percentage-of-population-vaccinated-march-15.html If the states with under 30% fully vaccinated were suffering major spikes or stuffed ICUs, then you might have a point about vaccine efficacy being proven in the real world. But that is not happening.
Then you can also look at this chart showing comparisons in Europe:
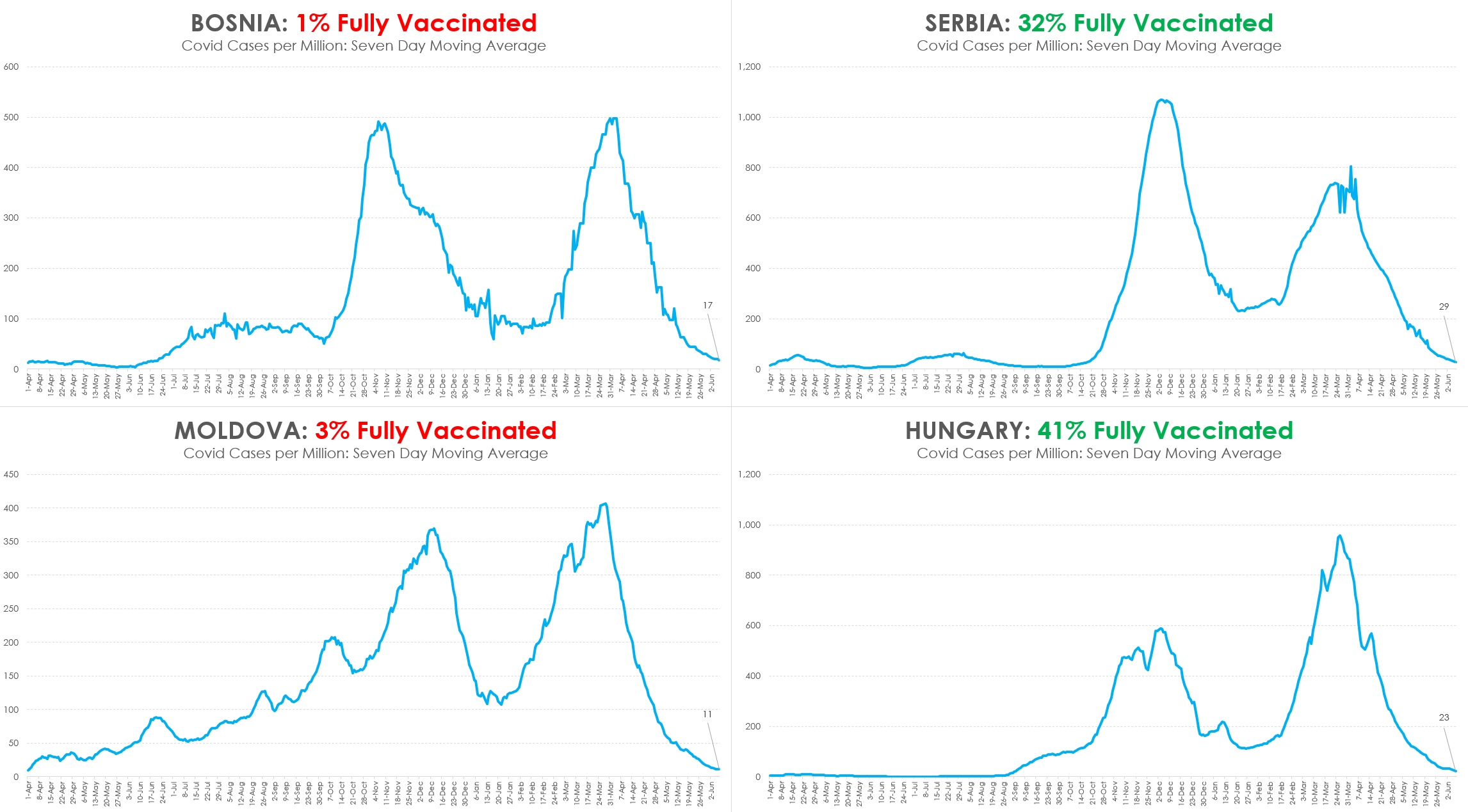
And the doctor who wrote this article made it clear that we expect cases and effects to decline, but that is how pandemics work. And he also expected that vaccine producers and supporters would attribute a natural occurrence to the vaccines. We also are already looking at “boosters” being required. Whereas naturally occurring immunity (probably 100 million or more already have been infected) lasts fro decades.
You published that in April 2021? I wonder if being incredibly wrong caused you to rethink your assumptions and sources of information or merely to double down.
Did the fact that they are pushing a 4th dose of a failed pharma product make you rethink any of yours, Jonathan Hill?
Using absolute rates for this is silly, and suspect. For example:
Seatbelts reduce chance of death by about 50%. Lets say no one wears a seatbelt, and that’s about 40,000 car deaths per year. So instead of 40,000 car deaths per year we would have 20,000 if everyone wore a seatbelt (50% relative reduction). However there are 320,000,000 people in the U.S. So really it only changes the car deaths from (40,000 / 320,000,000) * 100 = 0.0125% of the population per year, to (20,000 / 320,000,000) * 100 = 0.00625% of the population per year. This is an absolute risk reduction of just 0.00625%, sounds tiny, yet most people still do wear seatbelts, and 20,000 people’s lives are still saved because of it.
That’s not how this works. You are comparing to the entire population, but ARR is calculated based on inclusion in the experiment:
ARR (Absolute Risk Reduction) = CER – EER = 0.884% – 0.044% = 0.84% = 0.84/100 = 0.0084
So in your example, you would need to do an experiment following a specific number of people for a specified unit of time. You would have one group that wore seatbelts and another that did not. If you are looking to compare mortality, the Experimental Event Rate would be the seatbelt wearers and the Control Event Rate would be the non-seatbelt wearers. Your calculations would be based on the results of your experiment, not compared against all accidents or the entire population. Does that make sense to you?
I can appreciate the point that the author is trying to make but this is an incredibly flawed analysis.
The point that he is making is that the infection rate of the placebo test group over the study period implies minimal risk. Fair. This is a valid point, I believe.
The point about the effectiveness, just purely according to statistics, is nonsense. It makes a very critical error, it ignores compounding. A virus is not a single period organism, it spreads.
To illustrate, assume the rates of infection from the study groups and assume an R0 rate of 1 (each infected person gives it to 1 other person in a period) and assume 10 periods for argument’ sake (you can think of 10 weeks or 10 months or whatever you wish).
For the placebo you would have (1 + 0.884%)^10 percent of your population who have been infected.
For the vaccinated group it would be (1 + 0.044%)^10.
So what’s the difference? 8.8% of your population was infected vs 0.44%.
Over 20 periods 19.2% vs 0.9%.
You can argue about the risk-reward associated with the vaccine given real world mortality rates (and arguably front loaded excess mortality in 2020) and an arguably lower R0 rate now given all of the vaccinations but I think the article is very misleading for something that claims that the clinical trials are misleading.
Again, I appreciate the point and wish you all the best.
This point has been made before in response to other similar comments, and the point is that you, too, are making assumptions about spread which in turn makes assumptions about the raw data. The author of the article did not make any assumptions. He used the raw data of the Pfizer monograph to show how Pfizer came up with a 95 per cent relative risk reduction but that the same data yields an absolute risk reduction of less than 1per cent and a number needed to treat of 119. If you want to conduct additional statistical analyses, you have to use the same data. The whole point of the article is reporting bias.
“To date, there have been 33,217,718 Covid-19 recorded cases in the US and 593,282 recorded Covid-19 deaths. These statistics can be found here https://covidusa.net/ and their validity assumes that Covid cases have not been underestimated and Covid deaths have not been overestimated. If 2.77 million Covid-19 cases had been prevented by fully vaccinating every US citizen, the US would still have experienced approximately 30,447,780 Covid infections and by extrapolation 543,810 Covid deaths, a reduction of 49,472 deaths or 1.78% fewer Covid-19 deaths.”
This does not seem right..maybe someone can explain it to me. 20x the amount of people got covid in the placebo group compared to the vaxx.. so the amount of people getting the vaxx would have 20x less infection (by standards used). Roughly 33 million infections would have been around 1.65 million
Dear Russell Crane,
If you compare only the number of infected people within the two groups, you are essentially conducting a type of RRR, not an ARR. the 20 X difference is not 20 out of 100 but 20 out of roughly 18,000. 0.044% X 20 = 0.88% which is still <1%. To do it properly, you must use the NNT.
Here are my expanded calculations:
If the NNT to prevent one case of Covid infection is 119 and the population of the US is 330,000,000, dividing the population by 119 yields 2.77 million Covid infections. In other words, immunizing every American in the US would prevent 2.77 million Covid infections.
However, the US already experienced 33,217,718 infections. For simplicity, I assumed all of these infections occurred in an unvaccinated population.
33,217,718 – 2,770,000 = 30,447,718
Therefore, had every US citizen been vaccinated, 30,440,718 infections would have occurred instead of 33,217,718 infections.
We know that of those 33.2 M infections, 593,282 resulted in death.
By cross multiplying for X,
33,217,718 infections/593,282 deaths = 30,447,718 infections/X
X = (30,447,718,718 infections)(593,282 deaths)/33,217,718 infections = 543,810 deaths
593,282 deaths – 543,810 deaths = 49,472 fewer deaths had every American citizen been vaccinated with the Pfizer mRNA Covid-19 vaccine
By cross-multiplying again,
49,472 deaths/593,282 deaths = X/100
X = 4,947,200/593,282 = 8.3
With an NNT of 119, the Pfizer vaccine would have resulted in 8.3% fewer deaths, and not 1.78% as per my original calculation.
I do apologize for this error, but it does not change the fact that the vaccine would have had little impact both in the infection rate and the death rate had every US citizen been vaccinated.
For each individual vaccinated, the Absolute Risk Reduction is still 0.84% which means that the risk for getting infected after vaccination is 100% – 0.84% = 99.16%, and NOT 5% as the RRR implies.
Yes, some lives will be saved, but at what expense, and could we have done better with a different approach?
I agree with your calculations about ARR vs. RRR, and NNT, and that informing people of RRR only is misleading. However,because the end points of the trials were symptoms, not infections, I’m not sure why Mr. Spanakopitas and you talk about infections. The compounding could not be calculated using these ARR/RRR numbers. Nor could the RRR or ARR be applied to infections as you have done.
ARR for symptoms is rough and depends on likelihood of infection in first place, viral load one is exposed to, and vulnerability to disease. So for some people with higher risk. I don’t know how to best represent risk reduction. I think the Brown paper showed that FDA guidance is to inform about both, but I don’t know what people would make of that information without some explanation about relation to individual circumstance.
The vaccine companies and CDC claim the vaccines lower transmission because of lower viral loads, and I assume they do, but
I don’t know if that has been quantified.
I’ve read this, finally understand RRR etc, does prove vaccine halts infection, doesn’t prove it’s safe though. I’m in NZ, is it worth trying to network with church leaders here to alert their congregations to vaccine harm? Advice appreciated!
This confirms your article:
https://www.barnhardt.biz/2021/05/28/top-tier-medical-journal-the-lancet-blows-lid-off-of-vaccine-lie-pfizers-efficacy-rate-0-84-as-in-less-than-1-as-in-statistically-zero-in-other-words-these-injections/
Dear PX
You cannot argue real world experimental data with hypothetical arguments. The Pfizer study is a placebo controlled study. The methodologies in your hypothetical study examples are not placebo controlled. Therefore, you are comparing apples to oranges. The NNT is still 119, whether you immunize half the population or all of it or 1% of it. That does not change. You may be good in Math, but Statistics, Clinical Epidemiology and Experimental Methodology require much more than just Math.
The author is real funny. He talks about RRR and ARR correctly but he just switched the mathematical concepts around as if he’s never studied maths.
“1 In the vaccine group, 8/18,198 got Covid-19 infection (not death) = 0.044%. This is the EER (Experimental Event Rate)
2 In the Control (placebo) group, 162/18,325 got covid-19 infection (not death) = 0.884%.
This is the CER (Control Event Rate)
3 ARR (Absolute Risk Reduction) = CER – EER = 0.884% – 0.044% = 0.84% = 0.84/100 = 0.0084
4 RRR (Relative Risk Reduction) = ARR divided by CER or 0.84% divided by 0.884% = 0.95”
5 the ARR or Absolute Risk Reduction, which is 0.0084 or 0.84%, is actually less than 1%”
Imagine now I have developed a new drug.
I did experiments on two batches of patients with each batch consisting of 500000 random patients whose other factors such as age and sex are controlled.
In Batch A, I used the drug on all the 500000 patients, and 1 out of 500000 patients died from the disease.
In Batch B, I didn’t use the drugs on the 500000 patients, and 100 out of 500000 patients died from the disease.
Then we can similarly calculate the ARR and RRR in this case:
EER = 1/500000 = 0.0002%
CER = 100/500000 = 0.02%
ARR = 0.02%-0.0002% = 0.0198%
RRR = 0.0198%/0.02% = 99%
Now, if you tell me the drug is 0.00198% useful for treating the disease (which basically means it’s statistically not useful for treating the disease at all), how do you explain that out of the expected 100 fatalities, there are 99 people who could have died but didn’t?
Moreover, let’s repeat the experiment on 7 billion patients in each batch (i.e., the scenario where no one in this world takes this drug VS the scenario where everyone in this world takes this drug, supposing that everyone in this world has already got this particular disease). Because I’m using the same drug for this experiment, the EER and CER should be around the same.
The number of expected fatalities if everyone takes this drug = 7 billion X 0.0002% = 14000
The number of expected fatalities if no one takes this drug = 7 billion X 0.02% = 1400000
So this drug would practically save more than a million people’s life if everyone is sick but also takes the drug despite having an almost negligible ARR of 0.0198%.
In comparison, no one in this world is immune to the SARS-Cov-2 virus (which is similar to the case where everyone has got a peculiar sickness), and the Covid vaccine has an ARR of 0.84%, which is more than 40 times higher than that of the aforementioned imaginary drug that could save more than a million people’s lives.
So, in the author’s logic, the Covid vaccine would have been a “miracle” or a “panacea”, because it’s gonna save who-knows-how-many-million people’s lives (definitely more than enough to cover the 3.54 million Covid-related deaths that have occurred so far) if everyone takes the vaccine!!!
Lol. This is why looking at ARR for “efficacy” is useless. You must look at the RRR to get a correct sense of how effective a vaccine is.
Actually, you are completely off base on everything in this post, but we posted it because we try to avoid censorship. Except in the case of blatant heresy. That we censor. But this is science, and not dogma, so we allow it, even though we don’t agree with it.
One of the central figures in this worldwide dystopian mess, Bill Gates, says he has a favorite book. It is called “How to Lie with Statistics”:
https://www.gatesnotes.com/Books/How-to-Lie-with-Statistics
https://orthodoxchristiantheology.com/2020/12/20/does-orthodoxy-condemn-vaccinations/
Saint Paisios the Athonite in Spiritual Bravery in the chapter “The Signs of the Times” warned that “a vaccine has been developed for a new disease, which will be obligatory and people taking it will be marked [with 666]
Analysis of Pfizer’s Data
ARR (Absolute Risk Reduction) = CER – EER = 0.884% – 0.044% = 0.84% = 0.84/100 = 0.0084
RRR (Relative Risk Reduction) = ARR divided by CER or 0.84% divided by 0.884% = 0.95
0.95 is not 95%, because 0.884% is not 100%
!!!!
0.84% is the final answer statistical for ARR
My Dear Friend, Gabriel,
There is nothing wrong with the mathematical calculations or statistical analysis of the article. You may need to brush up a bit in these areas.
RRR (Relative Risk Reduction) = ARR divided by CER = 1% divided by 2% = ½=50%??????
1/2=50% only when 2=100%
1% divided by 2% = ½ -not important for statistics
it is not %, only 1/2, because % / %=1
here is the problem,the answer is not a pourcentage.this is a just a number.
1/2 is not 50%
ARR (Absolute Risk Reduction) = CER – EER = 2% – 1% = 1% this is correct
I have been schooled in the coming “New World Order” since the 1970s. A highly respected missionary (Protestant) traveled the world and investigated the world banking system and discovered their goal of ruling the entire world through monetary controls (See: The Day the Dollar Dies by Willard CAntalon). So I have seen this coming for a long time. When they tell me the “Vaccine” turns the body into a bioweapons factory, I believe them because of what I have been seeing and hearing for the 40+ years. The globalists have made their move. Whether they can pull it off remains to be seen.
I appreciated how this article reveals how statistics can be used to deceive the world. There was a statement near the end which raised an eyebrow:A much better and safer approach for travelers would be a negative Covid-19 test, whose accuracy, although not perfect, is far better than 1% or less.
The PCR test is fake. Terry Mullens, the inventor said it must not be used to diagnose disease because of the high rate of false positives. To suggest a negative PCR test is a better way to go does no service to anyone. Here is something for you to investigate: There is no virus and no proof it exists. It has never been isolated and studied. Nobody has a sample of an isolated virus, therefore they cannot have studied the genetic sequence. Isolated means it is alone, not mixed with anything else. Such a sample does not exist. We have been under a psychological operation long-planned and now incredibly well executed.
So some of us questioned that. The good doctor said that a positive test with symptoms meant you are sick with Covid, whereas a negative test and no symptoms means definitely not. We were suspicious of that answer given all the false positives and the role of the PCR tests in propagating this “pandemic.” In the end, we went with the article as submitted and let everyone make their own judgments. The lack of real world protection from the vaccinations is the main point, in any case.
My understanding was that this is a real virus and the per test had a very low rate of false positives but a high rate of false negatives, up to 30 per cent. Considering also how many people with Covid did not get tested during the first wave, because they were told not to for various reasons;plus the overestimation of Covid deaths, puts the mortality rate at a much lower number than what we are being told.
*Kary Mullis
https://www.youtube.com/watch?v=rXm9kAhNj-4
Excellent article. But unfortunately, I disagree with this: “If people are properly informed that their ineffective protection from a Covid vaccine is actually 1% or less, and not 95% as advertised, vaccine uptake would drop dramatically.” I don’t think the covid true believers would change their behavior a single iota. Sadly, they are long past the stage of caring about facts.
Agreed, but aren’t they already vaccinated? So for them, too late. But now we are dealing with kids, teens, and the people who have so far refused, but are now getting pressure from work. We really think this is going to fall apart, as information is becoming more widespread about side effects and lack of efficacy. We keep encouraging people to hold on, even if getting pressed by school or job.
The vaxx is safe and effective…at either killing you or sterilizing you.
Moral of article. Don’t take everything the gov’t tells you at “face value”.
Christ is risen!! You’re analysis and breakdown is greatly appreciated. This only reinforces my revulsion and distrust of the “miracle.” I’m deeply saddened and worried that many people I love have submitted because of fear. They’ve been terrorized for well over a year, and have given their trust to a bunch of snake oil salesmen. What will happen to long term has me concerned.